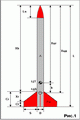
Проектирование сверхзвукового сопла

рекомендации по выбору формы сверхзвукового конического сопла ракетного двигателя

Задачи сопла ракетного двигателя для многих интуитивно понятны. Прежде всего, это нормировать площадь выхода реактивной струи для поддержания оптимального давления в камере сгорания. Во-вторых, организовать строго определенное направление истекания для задания нужного направления вектора тяги. И, наконец, разгон и повышение энергетики струи за счет использования эффектов сжимаемости.

Формально определение сопла звучит так: газовый канал переменного сечения, предназначенный для разгона рабочего тела для создания тяги.

Разговор пойдет в основном о простом коническом сверхзвуковом сопле, рис.1, получившее наибольшее распространение у любителей.

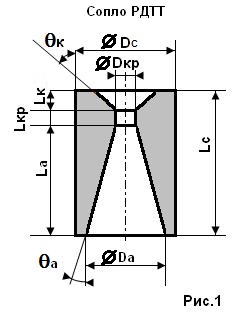Для начала определимся в понятиях. Канал сверхзвукового сопла состоит из входного конуса, или конфузора, самой узкой части, или критики, и выходного конуса - диффузора. Определяющими параметрами можно считать углы полураствора конусов конфузора θ_к и диффузора θ_а, диаметры критического сечения D_кр и выходного сечения D_а, или сечения среза.

В этой статье я не буду подробно останавливаться на выборе размеров критического сечения. Намечу только основной механизм проектирования.

Обычно у любителя нет особой возможности выбора корпусов для РДТТ. Есть какая-то труба из известного материала и известным пределом прочности σ.
Зная размеры трубы, а именно диаметр D и толщину стенки δ, по простой формуле рассчитывают предельно допустимое значение давления в двигателе:

P=2·σ·δ/(n·D),

где n - страховочный запас прочности, обычно берут 1,5-2. Далее в программе расчета параметров тяги, такой, например, как Rocki-motors, подбирают размеры и форму заряда в сочетании с диаметром критического сечения так, чтобы расчетное давление не превысило максимально допустимого для данной трубы. Форма заряда однозначно зависит от размеров корпуса. Диаметр заряда определяется диаметром трубы за вычетом толщины теплоизоляции и бронировки. Длина заряда тоже достаточно определенна, поскольку либо ограничена размерами трубы, либо размерами ракеты. Исходя из эмпирического правила для отдельной шашки заряда

L_ш=1.5–2.0 · D_ш ,

получаем, что подбор параметров мотора на основе максимально допустимого давления в основном ведется подбором критического сечения D_кр.

Определившись с критическим сечением сопла, можно приступать к проектированию его формы.

Вход продуктов сгорания осуществляется через входной сужающийся конус сопла - конфузор. Здесь нет особо строгих рекомендаций, и многие сопла имеют очень короткий конфузор или вообще не имеют его. Однако в научной литературе конфузор делать рекомендуют. В нем происходит разгон газового потока до звуковой скорости. Для уменьшения тепловой нагрузки на стенки конфузора угол полураствора берут в диапазоне

θ_к = 30–60°.

После конфузора поток проходит по критическому каналу. Возникает вопрос о длине критического канала L_кр. Общая рекомендация здесь простая - чем меньше, тем лучше. По технологическим причинам сделать очень коротким данный участок обычно не получается, поэтому любители исходят из правила

L_кр ≤ 0.5 · D_кр 

Из критики рабочее тело, то бишь продукты сгорания, попадают в диффузор. В расширяющемся конусе диффузора происходит разгон потока до сверхзвуковой скорости, предел которой определяется удельным импульсом мотора. От угла этого конуса зависит баланс разного рода энергетических потерь, таких как трение и рассеяние. Оптимальным считается угол полураствора в диапазоне

θ_а = 9–12°.

В теории длину диффузора L_а надо делать как можно длиннее, но на практике это означает возможность просто никуда не улететь из-за размеров сопла. Оказывается без особого ущерба можно ограничиться длиной, которая соответствует диаметру на срезе

D_a = 1.5–2.5 D_кр 

   Мы прошли по всему тракту сопла и в результате у нас вырисовались такие правила

Дотошный ракетчик может задаться вопросом, а как правильно осуществить переход от конфузора к критике и от критики к диффузору? На самом деле влияние формы этих переходов не критично. Лучше их слегка скруглить. Для педантов могу привести цифры из книги, которую я упоминал выше. Радиус скругления конфузор-диффузор лучше делать порядка 0,5–2D_кр, а радиус критика-диффузор - 0,5–3D_кр.

Приведенные рекомендации дают не большой диапазон для творчества, достаточно жестко определяя форму конического сопла. Однако они не являются догмой. Отступления от вышеуказанных правил допустимы, но при этом надо понимать, что характеристики сопла изменятся не в лучшую сторону. Если есть какая-то необходимость отступления, например, из-за ограничений по длине, то, прежде всего, надо постараться сохранить без изменений критику и диффузор.

P.S.
   Содержание может корректироваться и дополняться по мере накопления данных.
    В статье использованы материалы из книги Фархутдинов И. Х., Котельников А. В. "Конструкция и проектирование ракетных двигателей твердого топлива"

***