Оптимальный размер шашки

определение оптимального размера шашки заряда с внешней бронировкой

Речь пойдет о простых шашках заряда ТРТ с круглым каналом, имеющих бронировку с внешней стороны. Поверхность горения у них, соответственно, торцы и канал. Такие шашки наиболее распространены в любительских моторах с неразгораемыми соплами и применяются из-за технологической простоты и с целью получения максимально равномерного, распределения давления (а значит и тяги) в моторе по времени.

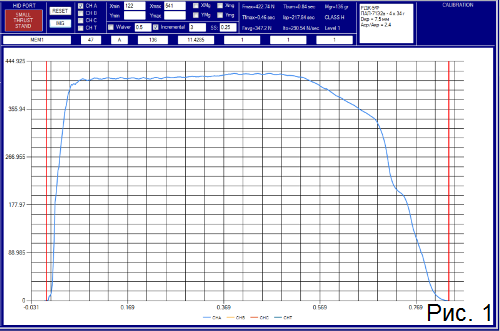
В идеале ракетчики стремятся к постоянному давлению в течении работы мотора, так называемой "полочке". Пример "полочки" показан на рис.1, её мне удалось получить на моторе РДК-5Ф. Примерно постоянное давление в процессе работы мотора позволяет максимально использовать возможности ракетного мотора. В этой статье я не буду вдаваться в подробные разъяснения этого факта, скажу только, что при том же суммарном импульсе можно получить наименьшее максимальное рабочее давление.

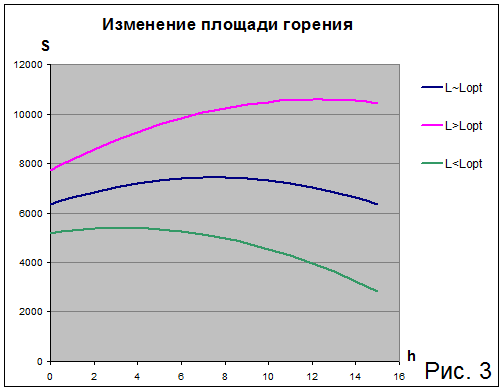
Получить "полочку" на шашках с внешней бронировкой и круглым каналом в теории нельзя, но можно организовать близкий к ней симметричный профиль горения с небольшим перепадом давления, это синяя кривая на рис.3. Для этого нужны определенные пропорции размеров шашки. Эти размеры обычно называют оптимальными. Поскольку диаметр шашки однозначно определяется диаметром корпуса мотора, а диаметр канала зависит от диаметра критики сопла, то поварьировать мы можем только длину шашки заряда. Начинающие ракетчики часто задают вопрос, как определить оптимальную длину шашки? Давайте разберемся, что это за оптимальные размеры, почему именно такие и как правильно выбрать длину.

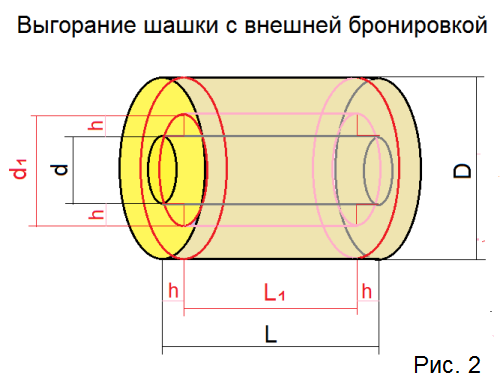
Процесс горения шашки диаметром D длиной L и диаметром канала d показан на рис.2. Мы исходим из стандартного предположения, что выгорание шашки во всех направлениях идет равномерно. Таким образом, при выгорании стенки топливного заряда на глубину h мы получаем новые размеры диаметра канала d₁=d+2h и длины заряда L₁=L-2h . На рис.2 новые размеры показаны красным.

Давайте сразу оговоримся, что случай L≤D-d на практике не приемлем, и мы его рассматривать не будем. Это означает, что шашка должна полностью выгорать раньше по диаметру, чем по длине для обеспечения прочности и целостности заряда.

Очевидно, что давление в моторе непосредственно зависит от площади горения. Меняется площадь - меняется давление. Давайте тогда и проанализируем, как меняется площадь в процессе горения шашки. Суммарная площадь горения шашки

S=π(D²-d²)/2 +πdL

После выгорания слоя h получаем новую площадь горения

S₁=π(D²-d₁²)/2 +πd₁L₁

Подставляя d₁=d+2h и L₁=L-2h, получаем зависимость площади горения от толщины слоя h

S(h)=π/2D²-π/2(d+2h)²) +π(d+2h)(L-2h)

Раскрыв скобки и пекомпоновав, получаем в таком виде

S(h)=π/2(D²-d²+2dL)+2π(-3h²-2dh+Lh)

Я специально записал в виде такой суммы. Первое слагаемое, очевидно, константа, а второе слагаемое квадратичная функция, или

S(h)=Const+f(h)

Причем заметим, что определяющей является константа, но она неизменна от h и значит от времени, а параболическая добавка f(h) - это та часть, которая меняется по времени и которую мы должны как-то оптимизировать. Сначала давайте просто посмотрим, как ведет себя функция S(h) при разных соотношениях L/D. На рис.3 видно, что при больших длинах шашки площадь горения ведет себя прогрессивно, при маленьких длинах наоборот регрессивно. Но при некотором соотношении площадь меняется не сильно и к концу горения такая же, как в начале. Понятно, что это и есть некоторое оптимальное распределение. Очевидно также, что это влияние квадратичной добавки. Парабола имеет наименьший прирост значения в районе своего экстремума, в данном случае максимума. Давайте вспомним школу и как записывается условие для экстремума функции, т.е. приравняем первую производную к нулю

f '(h)=-6h-2d+L=0

Что нам дает эта формулина? Дает она нам возможность подвигать точку максимума по толщине выгоревшего слоя. А где нам выгодно иметь точку максимума? Чем ближе эта точка к центру кривой S(h), тем лучше. Это потому, что именно в районе точки максимума прирост значений параболы минимален, и именно такое положение точки максимума позволяет максимально отсечь боковые ветви параболы. Центр кривой S(h) соответствует выгоранию половины стенки заряда, или условию

h=(D-d)/4

Подставляем это условие в предыдущую формулу, получаем искомую пропорцию

L = 3/2 D + 1/2 d

Это и есть оптимальная длина шашки заряда. Если учесть, что чаще всего при производстве шашек придерживаются соотношения d=D/3 или близкого к этому, можно еще больше упростить результирующую формулу

L = 10/3 D ≈ 1.67D

Справедливости ради надо заметить, что характеристика мотора по давлению строится в зависимости от времени, а не толщины слоя выгорания h. А толщина сгорающего слоя в единицу времени зависит от скорости горения u, или h=ut. То есть наши рассуждения строго справедливы в случае постоянной скорости горения. Однако в данном случае, когда давление меняется мало, скорость горения примерно постоянна.

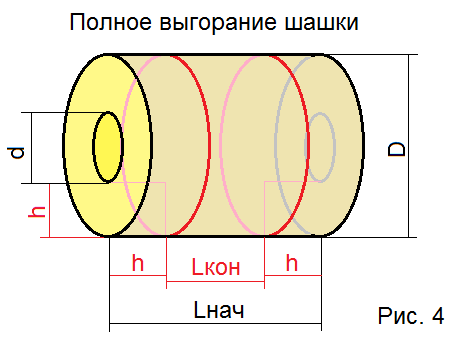
Честно говоря, с высоты проведенного нами анализа, задачу оптимизации размеров шашки можно решить еще проще. Мы уже выяснили, почему нам интересен именно симметричный профиль горения, а значит нам достаточно прописать условие равенства площади горения в начале процесса и в конце процесса. Соответствующая картинка полного выгорания шашки покзана на рис.4.

В начале площадь горения, как мы уже прописывали

S_нач=π(D²-d²)/2 +πdL

В конце, когда торцов уже нет

S_кон=πD(L-2h)

Ясно, что в конце горения толщина сгоревшего слоя равна толщине стенки заряда h=(D-d)/2, тогда

S_кон=πD(L-(D-d))

Из условия S_нач=S_кон

(D²-d²)/2 +dL=D(L-(D-d))

Преобразуем под общий множитель (D-d)

(D-d)(D+d)/2 +D(D-d)=L(D-d)

Cокращаем его, раскрываем скобки, группируем и получаем наше любимое соотношение для оптимальной длины

L = 3/2 D + 1/2 d

Итак, мы решили задачку оптимизации размеров шашки заряда аж двумя способами. Понятно, что это теория. На практике происходят более тонкие процессы. Скорость горения немного плавает, да и предположение о равномерном послойном выгорании не совсем верно. Однако именно практика показывает, что полученное нами соотношение хорошо работает. Я раньше всегда рекомендовал придерживаться правила L=1.5-2D. Если внимательно посмотреть на формулу оптимума, можно заметить, что этот диапазон соответствует крайним случаям при d=0 и d=D. Касательно выбора диаметра канала d, то тут главное не делать его меньше диаметра критики сопла, т.е. d≥dкр. Повторюсь, обычно берут d≈D/3, тогда формула для оптимальной длины упрощается до соотношения L=1.67D.

Как-то так.

/24.11.2016 kia-soft/

***